题目描述
风风和万万想去旅游,他们正在乘火车前往目的地。在路上,风风发现自己的包里有一个刚买的魔方。这是一个 n 阶魔方,有六个面。于是他们俩想打个赌,让两个人都来猜猜这个魔方有多少块,看谁最接近。风风想要赢过万万,就需要你的帮助,你要帮他算出正确答案。他想知道这个魔方有几块,也就是求这个魔方的棱块、角块、中心块共有多少。
如果你还不知道棱块、角块、中心块是什么,别担心,可以接着往下看。
下图中,橙色部分是角块,蓝色部分是棱块,紫色部分是中心块。角块就是顶点上的几块,棱块就是每条棱上两个角块中间的几块,中心块就是除了角块和棱块的剩余几块。角块数 + 棱块数 + 中心块数 ,就是魔方总共的块数。



如果你还不知道棱块、角块、中心块是什么,别担心,可以接着往下看。
下图中,橙色部分是角块,蓝色部分是棱块,紫色部分是中心块。角块就是顶点上的几块,棱块就是每条棱上两个角块中间的几块,中心块就是除了角块和棱块的剩余几块。角块数 + 棱块数 + 中心块数 ,就是魔方总共的块数。



输入
一行,一个整数, n 。代表这是一个几阶魔方。
输出
一行,一个整数。代表这个魔方有多少块。
样例输入 Copy
2
样例输出 Copy
8
提示
所有数据保证在 int 以内,均为正整数。
注:本题不只有一种解法。
n != 1( 不考虑有 1 阶魔方的情况 )
在正方体中,有 6 个面,8 个顶点,12 条棱。
魔方就可以看成一个正方体。正方体上平平的部分是正方体的面,两条面相交的边就是正方体的棱,三条棱相交的点就是正方体的顶点。
 图中,黄色部分是正方体的一个面,橙色部分是正方体的一条棱,蓝色部分是正方体的一个顶点。
图中,黄色部分是正方体的一个面,橙色部分是正方体的一条棱,蓝色部分是正方体的一个顶点。
接下来,是对样例的计算和一点点提示。
除此之外,再额外举一个例子。
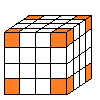

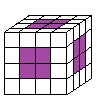
因为正方体共有 8 个顶点,也就是 8 个角,所以这个魔方有 8 个角块。
因为正方体共有 12 条棱,在这个魔方中每条棱上有 2 个棱块,12 × 2 = 24 ( 块 ) ,所以这个魔方有 24 个棱块。
因为正方体共有 6 个面,在这个魔方中每个面上有 4 个中心块,6 × 4 = 24 ( 块 ) ,所以这个魔方有 24 个中心块。
因为在一个魔方中,魔方的总块数 = 魔方的角块数 + 魔方的棱块数 + 魔方的中心块数 ,8 + 24 + 24 = 56 ( 块 ) ,所以这个魔方共有 56 块。
故输出 56 。
注:本题不只有一种解法。
n != 1( 不考虑有 1 阶魔方的情况 )
在正方体中,有 6 个面,8 个顶点,12 条棱。
魔方就可以看成一个正方体。正方体上平平的部分是正方体的面,两条面相交的边就是正方体的棱,三条棱相交的点就是正方体的顶点。
 图中,黄色部分是正方体的一个面,橙色部分是正方体的一条棱,蓝色部分是正方体的一个顶点。
图中,黄色部分是正方体的一个面,橙色部分是正方体的一条棱,蓝色部分是正方体的一个顶点。 接下来,是对样例的计算和一点点提示。
样例输入:2 样例输出:82 阶魔方,有 8 个角块,0 个棱块,和 0 个中心块,8 + 0 + 0 = 8 ( 块 ),所以 2 阶魔方总共有 8 块。
除此之外,再额外举一个例子。
样例输入:4 样例输出:56是一个 4 阶魔方。



因为正方体共有 8 个顶点,也就是 8 个角,所以这个魔方有 8 个角块。
因为正方体共有 12 条棱,在这个魔方中每条棱上有 2 个棱块,12 × 2 = 24 ( 块 ) ,所以这个魔方有 24 个棱块。
因为正方体共有 6 个面,在这个魔方中每个面上有 4 个中心块,6 × 4 = 24 ( 块 ) ,所以这个魔方有 24 个中心块。
因为在一个魔方中,魔方的总块数 = 魔方的角块数 + 魔方的棱块数 + 魔方的中心块数 ,8 + 24 + 24 = 56 ( 块 ) ,所以这个魔方共有 56 块。
故输出 56 。